Коэффициент теплового расширения

Точные расчеты тепловой нагрузки

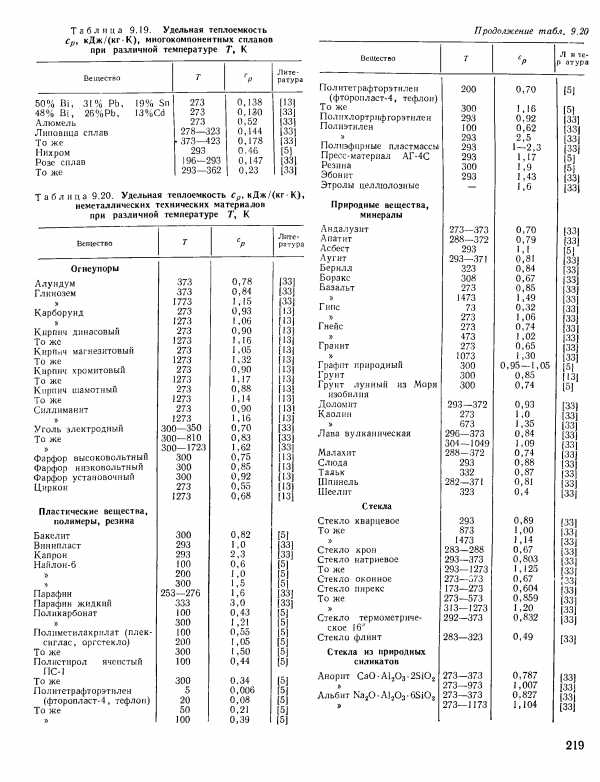
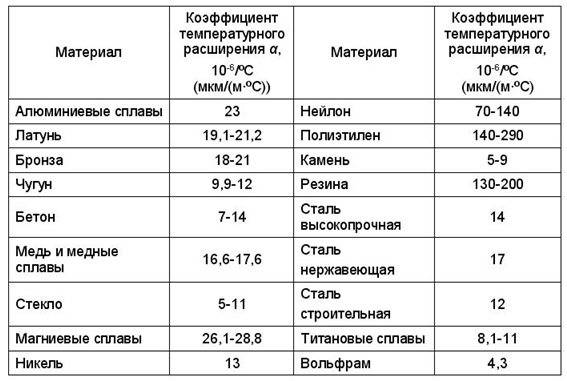
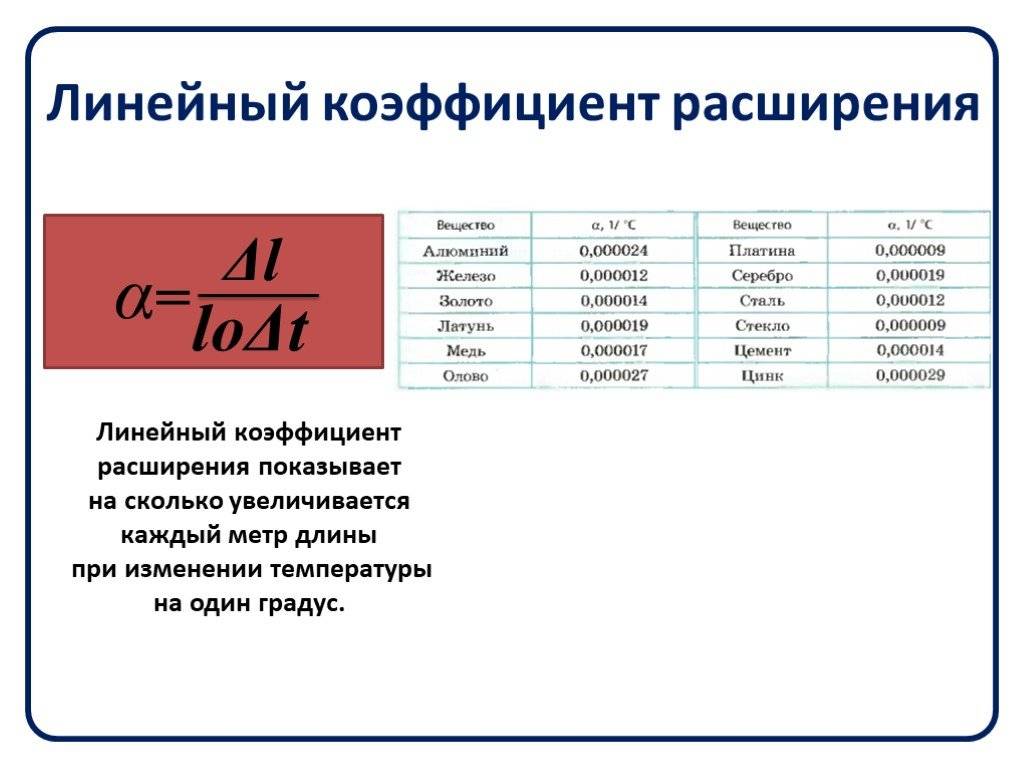
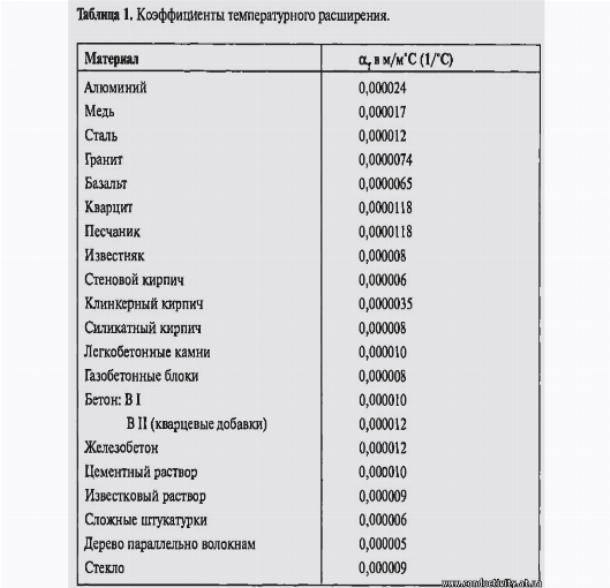
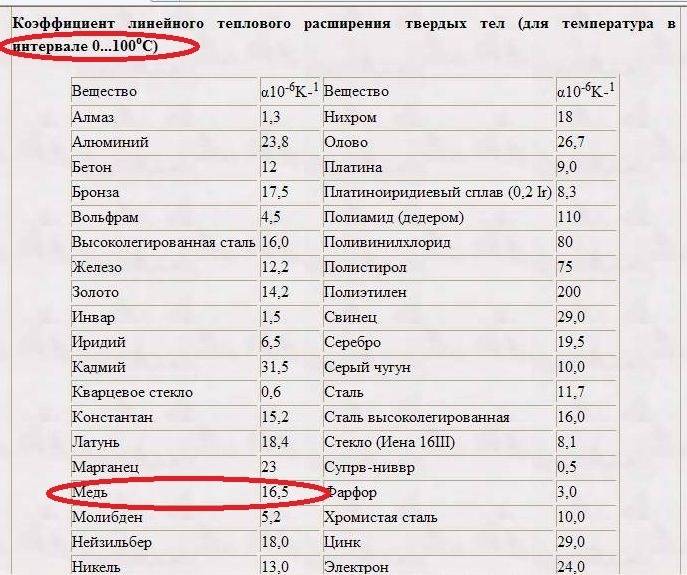
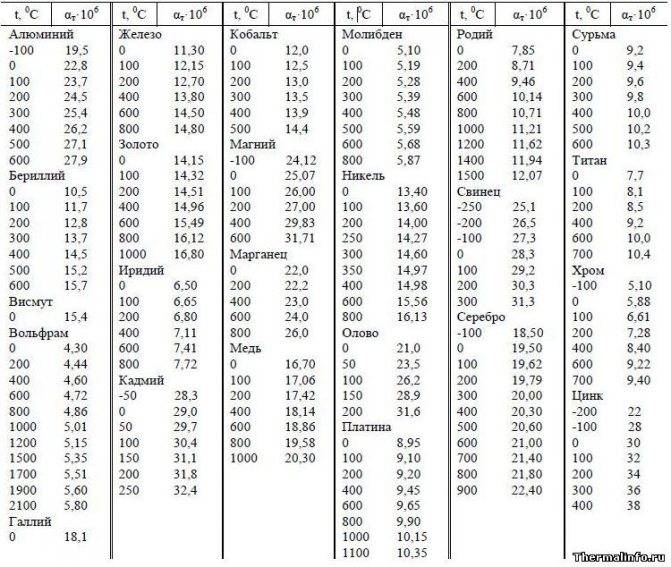
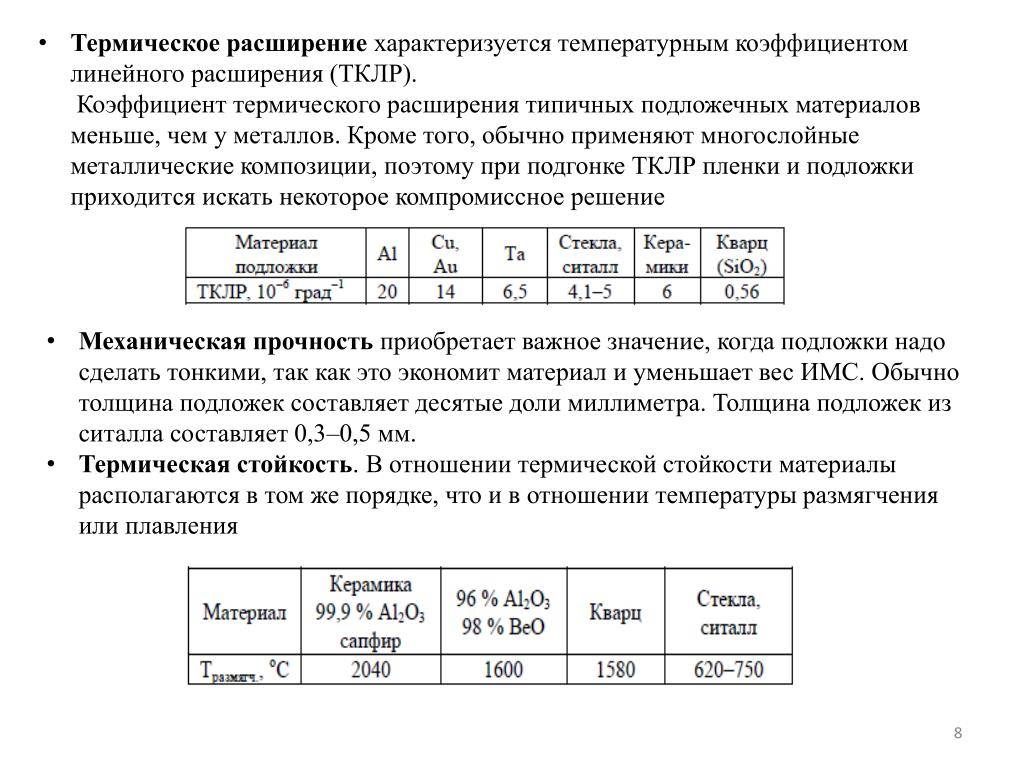
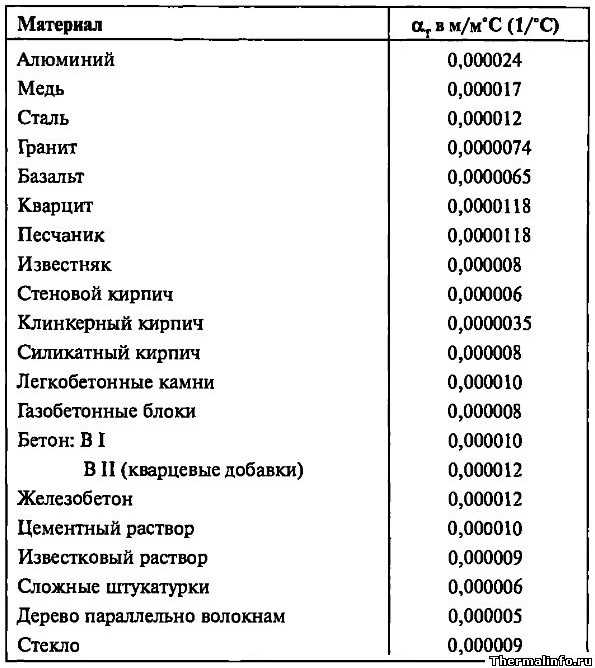
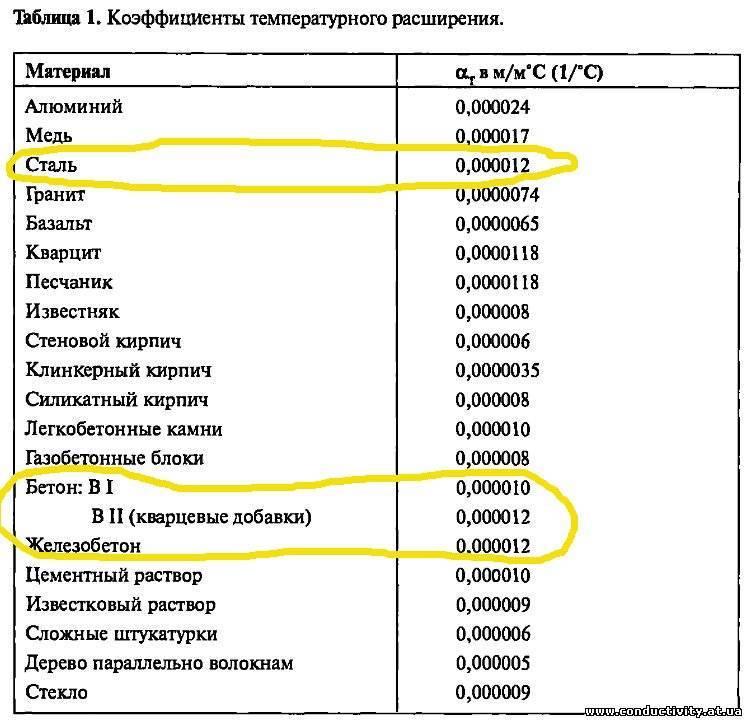
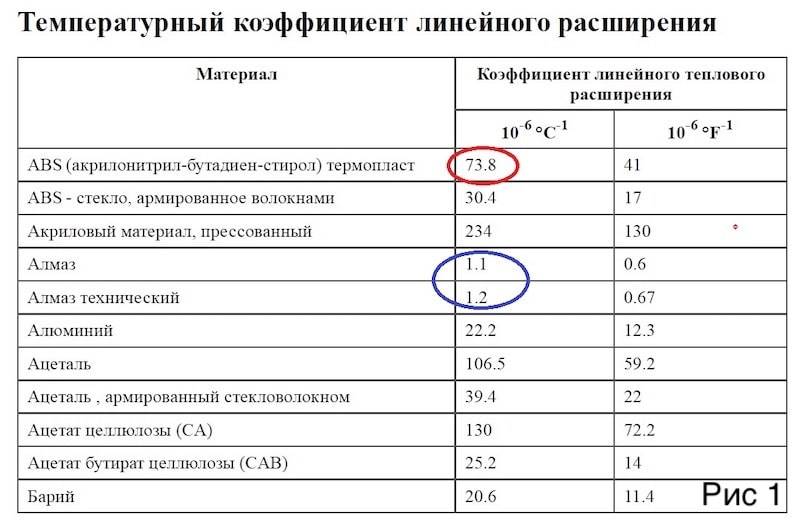
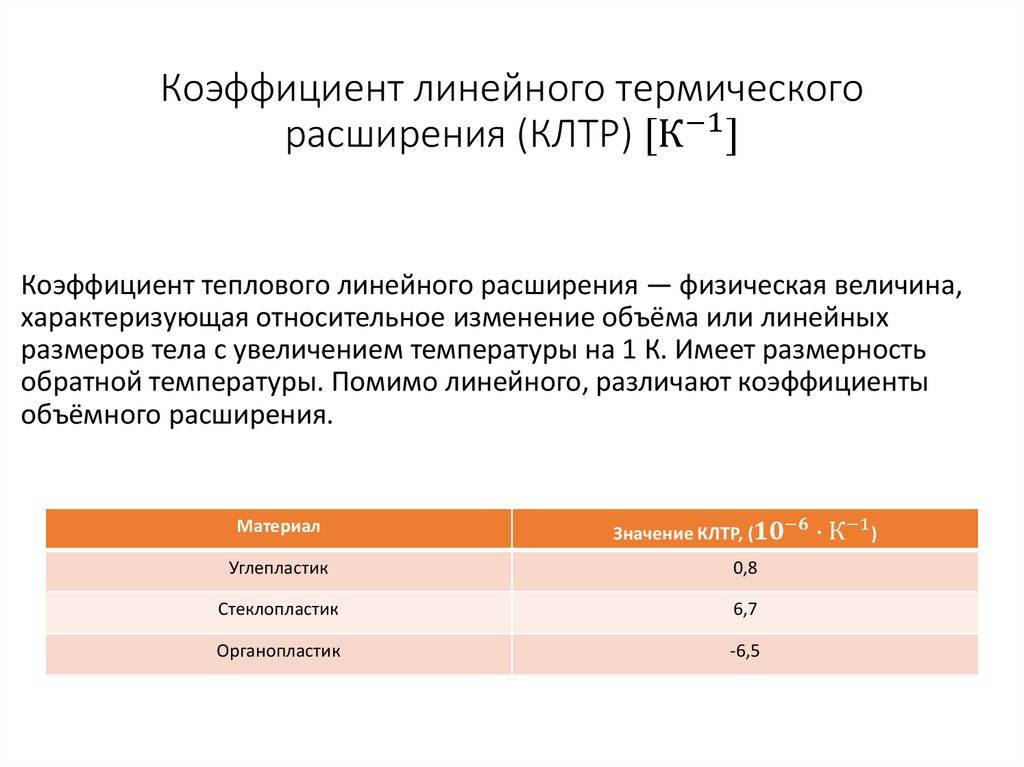
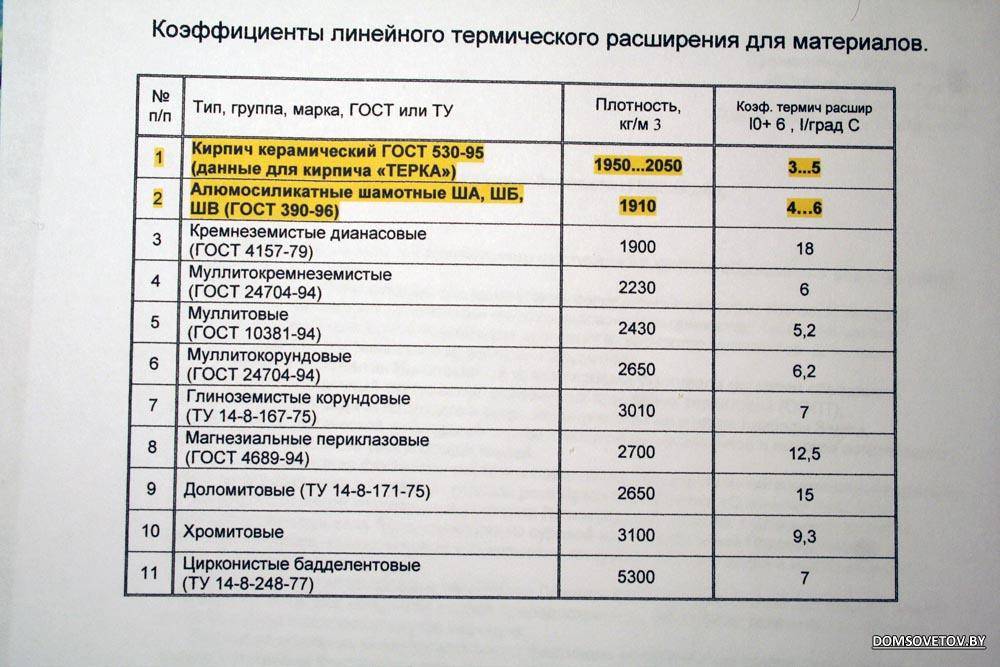
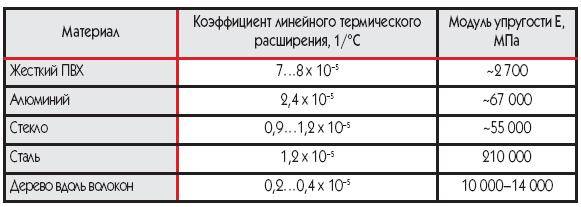
Значение теплопроводности и сопротивление теплопередачи для строительных материалов

Но все же этот расчет оптимальной тепловой нагрузки на отопление не дает требуемую точность вычисления. Он не учитывает важнейший параметр – характеристики здания. Главной из них является сопротивление теплопередачи материал изготовления отдельных элементов дома – стен, окон, потолка и пола. Именно они определяют степень сохранения тепловой энергии, полученной от теплоносителя системы отопления.

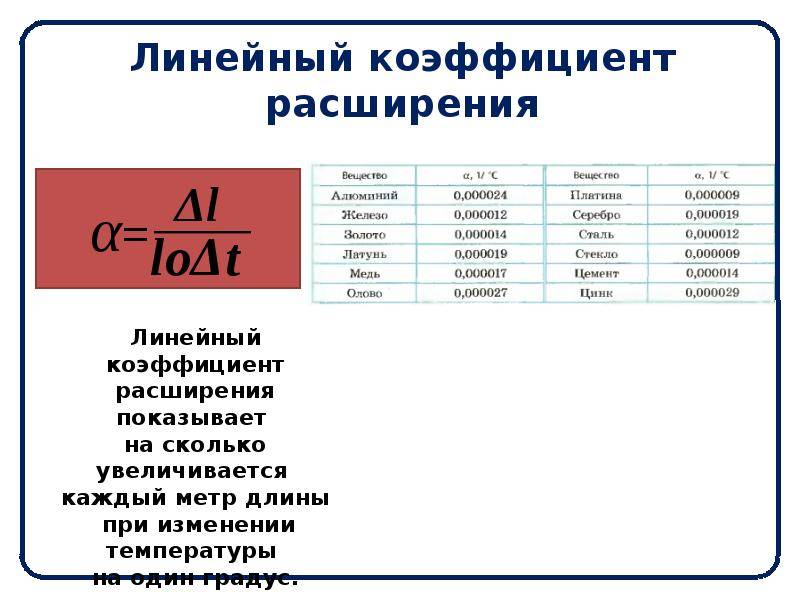
Что же такое сопротивление теплопередачи (R )? Это величина, обратная теплопроводности (λ ) – возможности структуры материала передавать тепловую энергию. Т.е. чем больше значение теплопроводности – тем выше тепловые потери. Для расчета годовой нагрузки на отопление воспользоваться этой величиной нельзя, так как она не учитывает толщину материала (d ). Поэтому специалисты используют параметр сопротивление теплопередачи, который вычисляется по следующей формуле:

Расчет по стенам и окнам

Сопротивление теплопередачи стен жилых зданий

Существуют нормированные значения сопротивления теплопередачи стен, которые напрямую зависят от региона, где расположен дом.

В отличие от укрупненного расчета нагрузки на отопление сначала нужно вычислить сопротивление теплопередачи для наружных стен, окон, пола первого этажа и чердака. Возьмем за основу следующие характеристики дома:

Площадь стен – 280 м². В нее включены окна – 40 м² ;
Материал изготовления стен – полнотелый кирпич (λ=0.56 ). Толщина наружных стен – 0,36 м. Исходя из этого рассчитываем сопротивление телепередачи — R=0.36/0.56= 0,64 м²*С/Вт ;
Для улучшения теплоизоляционных свойств был установлен наружный утеплитель – пенополистирол толщиной 100 мм. Для него λ=0,036. Соответственно R=0,1/0,036= 2,72 м²*С/Вт ;
Общее значение R для наружных стен равно 0,64+2,72= 3,36 что является очень хорошим показателем теплоизоляции дома;
Сопротивление теплопередачи окон — 0,75 м²*С/Вт (двойной стеклопакет с заполнением аргоном).

Фактически тепловые потери через стены составят:

(1/3,36)*240+(1/0.75)*40= 124 Вт при разнице температуры в 1°С

Температурные показатели возьмем такие же, как и для укрупненного вычисления нагрузки на отопление +22°С в помещении и -15°С на улице. Дальнейший расчет необходимо делать по следующей формуле:

Расчет по вентиляции

Затем необходимо вычислить потери через вентиляцию. Общий объем воздуха в здании составляет 480 м³. При этом его плотность примерно равна 1,24 кг/м³. Т.е. его масса равна 595 кг. В среднем за сутки (24 часа) происходит пятикратное обновление воздуха. В таком случае для вычисления максимальной часовой нагрузки для отопления нужно рассчитать тепловые потери на вентиляцию:

(480*40*5)/24= 4000 кДж или 1,11 кВт/час

Суммируя все полученные показатели можно найти общие тепловые потери дом:

Таким образом определяется точная максимальная тепловая нагрузка на отопление. Полученная величина напрямую зависит от температуры на улице. Поэтому для расчета годовой нагрузки на отопительную систему нужно учитывать изменение погодных условий. Если средняя температура в течение отопительного сезона составляет -7°С, то итоговая нагрузка на отопление будет равна:

(124*(22+7)+((480*(22+7)*5)/24))/3600)*24*150(дней отопительного сезона)=15843 кВт

Меняя температурные значения можно сделать точный расчет тепловой нагрузки для любой системы отопления.

К полученным результатам нужно прибавить значение тепловых потерь через крышу и пол. Это можно сделать поправочным коэффициентом 1,2 – 6,07*1,2=7,3 кВт/ч.

Полученная величина указывает на фактические затраты энергоносителя при работе системы. Существует несколько способов регулирования тепловой нагрузки отопления. Наиболее действенный из них – уменьшение температуры в комнатах, где нет постоянного присутствия жильцов. Это можно осуществить с помощью терморегуляторов и установленных датчиков температуры. Но при этом в здании должна быть установлена двухтрубная система отопления.

Для вычисления точного значения тепловых потерь можно воспользоваться специализированной программой Valtec. В видеоматериале показа пример работы с ней.

Анатолий Коневецкий, Крым, Ялта

Уважаемая Ольга! Извините,что обращаюсь к Вам еще раз. Что-то у меня по Вашим формулам получается немыслимая тепловая нагрузка: Кир=0,01*(2*9,8*21,6*(1-0,83)+12,25)=0,84 Qот=1,626*25600*0,37*((22-(-6))*1,84*0,000001=0,793 Гкал/час По укрупненной формуле, приведенной выше, получается всего 0,149 Гкал/час. Не могу понять, в чем дело? Разъясните пожалуйста! Извините за беспокойство. Анатолий.

Анатолий Коневецкий, Крым, Ялта

Примечания и ссылки

Джон Фредерик Най , Физические свойства кристаллов , Париж, Данод,1961 г.
(in) П. Пауфлер и Т. Вебер, « » , Eur. J. Mineral. , т. 11, п о 4,1991 г., стр. 721–730
(in) С. М. Джессен и Х. Кюпперс, ” Точность тензоров теплового расширения триклинных и моноклинных кристаллов ” , J. Appl. Cryst. , т. 24, п о 3,1991 г., стр. 239-242 ( DOI )
(in) Дэвид Р. Лид, Справочник CRC по химии и физике , Бока-Ратон, CRC Press,2009 г., 90- е изд. , 2804 с. , Твердый переплет ( ISBN 978-1-4200-9084-0 )
(in) Л.Д. Ноай, Х.-Х. Пенг, Дж. Старкович и Б. Данн, « Термическое расширение и фазообразование ZrW ₂ O _8.Аэрогели » , Chem. Матер. , т. 16, п о 7,2004 г., стр. 1252–1259 ( DOI )
(in) Дж. Дж. Редхаммер Г-н Мерц Г. Типпельт, К. Спарта, Г. Рот, В. Тройтманн, В. и Г. Лоттермозер Амтхауэр, « Уточнение кристаллической структуры в зависимости от температуры и мессбауэровская спектроскопия 57 Fe для Cu ₂ Fe ₂ Ge. ₄ O ₁₃ » , Acta Cryst. В , т. 63, п о 1,2007 г., стр. 4-16 ( DOI )
(in) К. Спарта, Дж. Дж. Редхаммер, П. Руссель, Г. Хегер, Г. Рот, П. Лемменс, А. Ионеску, г-н Гроув, Г. Гюнтеродт, Ф. Хюнинг, Х. Люкен, Х. Кагеяма, К. Онидзука, Ю. Уэда, “ Структурный фазовый переход в 2D спин-димерном соединении SrCu ₂ (BO ₃ ) _2. » , Eur. Phys. J. B , т. 19, п о 4,2001 г., стр. 507-516 ( DOI )
(in) Г-н Зема , SC Тарантино и AM Каллегари , « Температурное поведение либетенита от комнатной температуры до обезвоживания » , Mineralogical Magazine , vol. 74, п о 3,2010 г., стр. 553-565 ( DOI )

§ 9.2. Тепловое линейное расширение

Глава 9. Тепловое расширение твердых и жидких тел

Применительно к твердым телам, форма которых при изменении температуры (при равномерном нагревании или охлаждении) не меняется, различают изменение линейных размеров (длины, диаметра и т. п.) — линейное расширение и изменение объема — объемное расширение, У жидкостей при нагревании форма может меняться (например, в термометре ртуть входит в капилляр). Поэтому в случае жидкостей имеет смысл говорить только об объемном расширении.

Опыт показывает, что при небольших изменениях температуры изменение линейных размеров твердого тела прямо пропорционально изменению температуры (рис. 9.3). Так как удлинение при нагревании (или укорочение при охлаждении) зависит также от первоначальной длины тела, удобнее рассматривать не само удлинение тела, а относительное удлинение: отношение увеличения длины ωl = l — l0 к первоначальной длине l0. Относительное удлинение пропорционально изменению температуры ωt = t — t0:

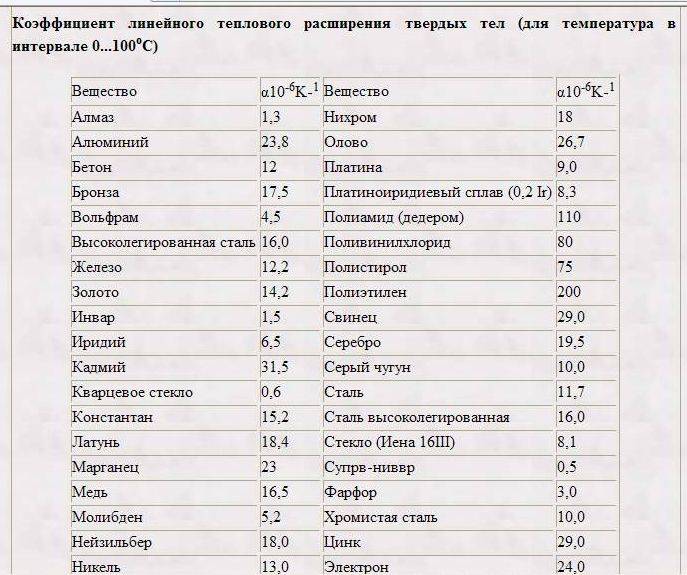
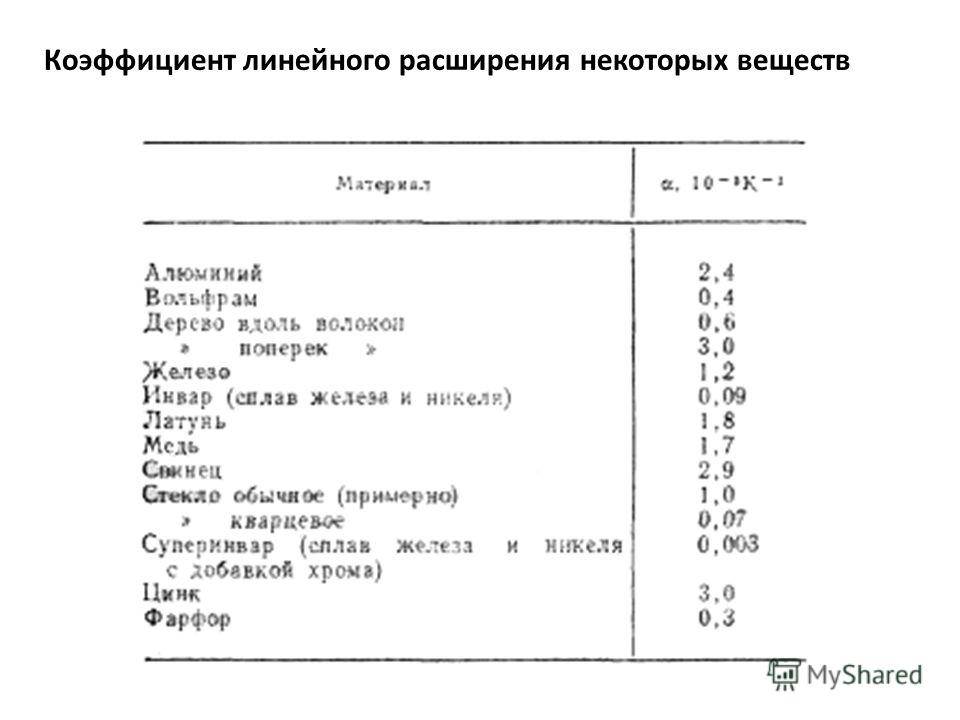
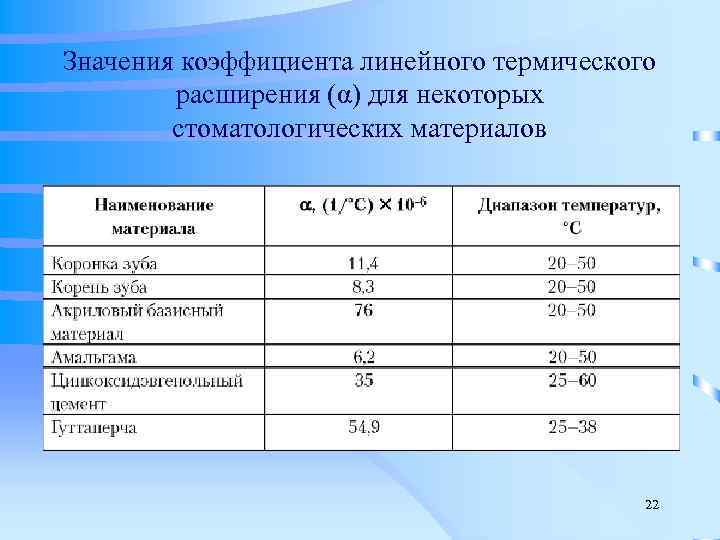
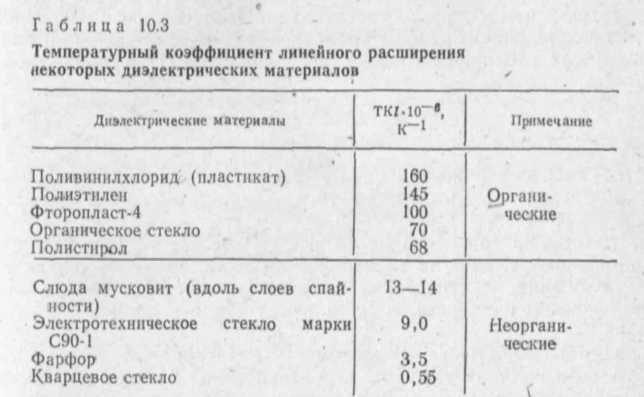
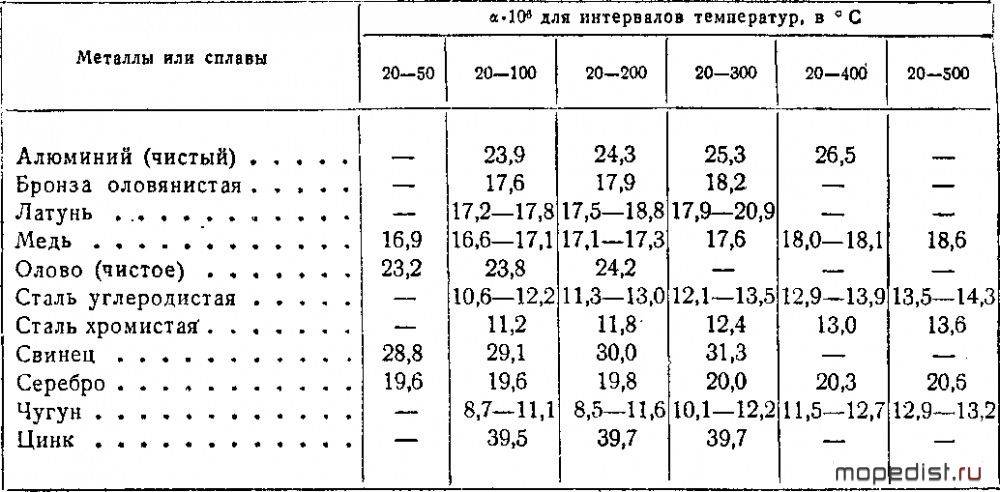
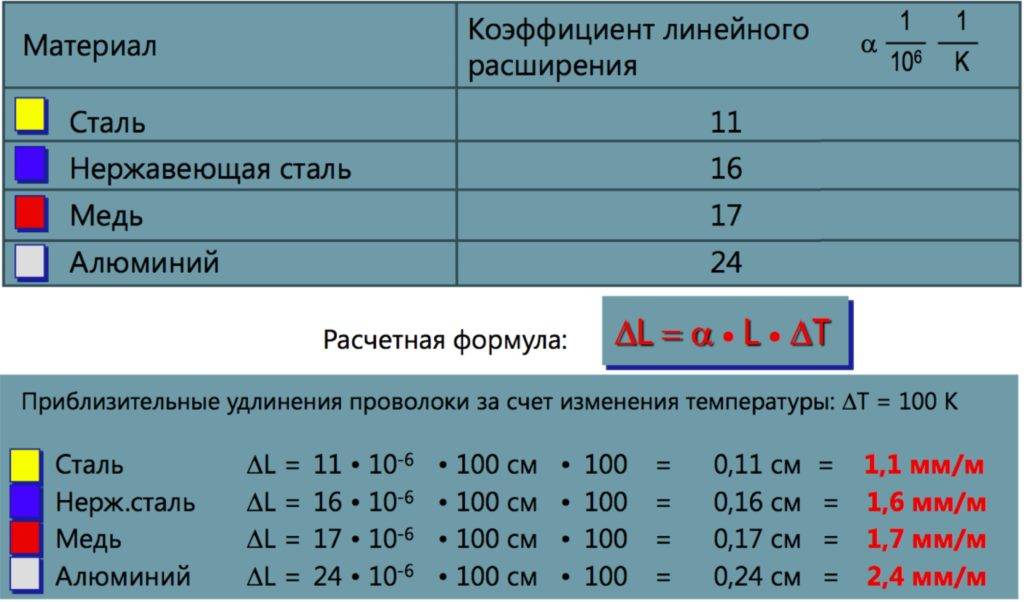
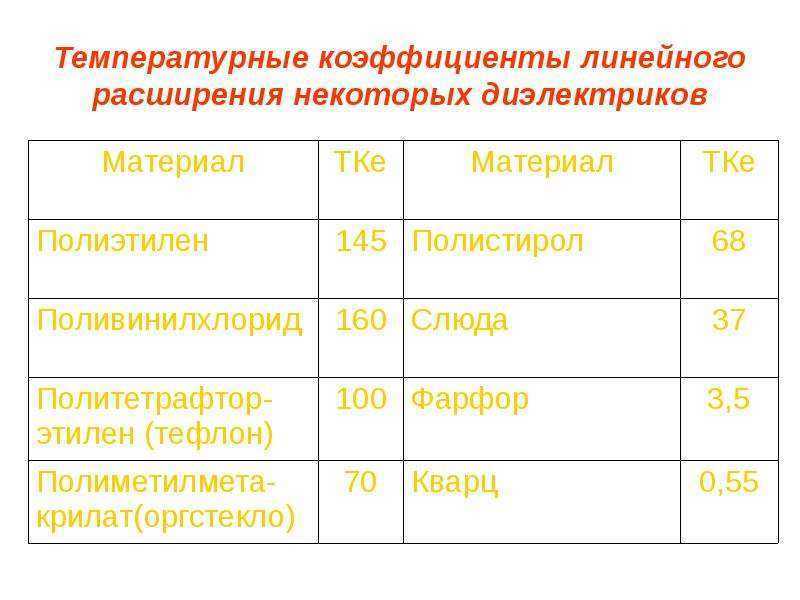
Коэффициент пропорциональности α1 называют температурным коэффициентом линейного расширения. Он показывает, на какую долю своего первоначального значения изменяются линейные размеры тела при нагревании его на 1 К. Коэффициент линейного расширения зависит от природы вещества, а также от температуры. Однако, если рассматривать изменения температуры в не слишком широких пределах, зависимостью α1 от температуры можно пренебречь и считать температурный коэффициент линейного расширения величиной постоянной для данного вещества. Для большинства веществ этот коэффициент мал, его значения составляют 10-5—10-6К-1.

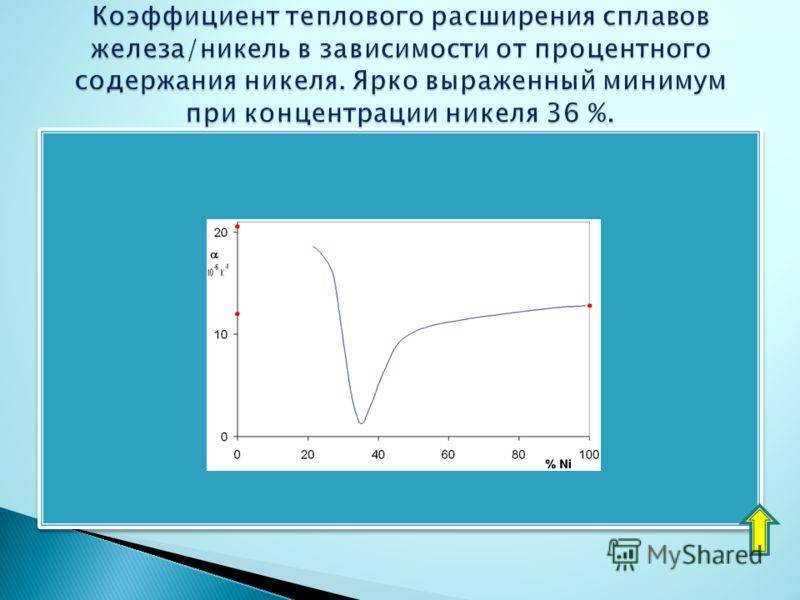
Особенно мал коэффициент линейного расширения в диапазоне температур от -30 до +100 °С у инвара (сплав железа и никеля). Поэтому инвар применяют для изготовления точных инструментов, используемых при определении размеров тел. Линейные размеры самого инструмента из инвара мало зависят от колебаний температуры.

Линейные размеры тела, как вытекает из формулы (9.2.1), зависят от изменения температуры следующим образом:

l = l0(1 + α1Δt). (9.2.2)

В формулах (9.2.1) и (9.2.2) обычно начальное значение температуры полагают равным нулю (t0 = 0 °С) и соответственно t0 считают длиной тела при этой температуре. На практике же начальная температура тела далеко не всегда бывает равна 0 °С. Тогда расчет длины тела при любой температуре можно выполнить так. Пусть при температуре t1 длина тела равна l1, а при температуре t2 она равна l2. Тогда, считая начальную температуру t0 = 0 °С, имеем

l1 = l0(1 + α1t1), l2 = l0(1 + α1t2).

Отсюда

Однако, учитывая, что значение α1 очень мало, формулу (9.2.3) можно упростить. Умножив числитель и знаменатель на 1 — α1t1, получим

Ввиду малости коэффициента α1 члены, содержащие малы по сравнению с членом, в который входит α1 в первой степени (точнее, ). Поэтому их можно отбросить. В результате формула для вычисления длины l2 оказывается более простой и достаточно точной для инженерной практики:

Решая задачи с учетом теплового линейного расширения тел, необходимо иметь в виду, что при изменении температуры меняется не только длина, но и все другие линейные размеры тела. Так, у круглого стержня при нагревании увеличивается диаметр, и притом во столько раз, во сколько увеличивается длина стержня. У пластинки в одно и то же число раз увеличиваются длина, ширина и толщина. Если начертить на пластинке какую-нибудь линию, то длина этой линии при нагревании увеличится в такое же число раз. У окружности увеличатся ее длина и диаметр.

При нагревании пластинки, имеющей круглое отверстие, диаметр отверстия тоже увеличится. Дело в том, что при равномерном нагревании в теле не возникают силы упругости. Поэтому расширение происходит так, как если бы пластинка была сплошной. Точно так же увеличивается при нагревании диаметр гайки, размеры раковины в толще металлической отливки и т. д.

В справедливости сказанного можно убедиться на опыте с металлическим шаром, о котором уже шла речь в § 9.1. Шар застревает в кольце, если его нагреть, и проходит с большим зазором, если нагреть кольцо. Наоборот, при охлаждении кольца шар застревает, а охлаждение шара увеличивает зазор между ним и кольцом.

Линейные размеры твердых тел увеличиваются прямо пропорционально росту температуры.

Расширение, а не сокращение

Почему при нагревании материя расширяется? Все дело в форме типичного потенциала частичек. Если они расположены в твердых объектах и жидкостях, то постоянно ощущают наличие соседних элементов. В математике выражается как потенциальная кривая. На нижнем рисунке видно, что этот межчастичный потенциал выглядит как асимметрия. Отметьте, что на коротких дистанциях она становится более крутой. На диаграмме (b) видно, что с нагревом вещества средняя дистанция частичек увеличивается. Очень редко можно встретить материал, который при нагреве сожмется или сохранит форму. Эффект ограничивается по размеру и осуществляется только в определенных температурных диапазонах.

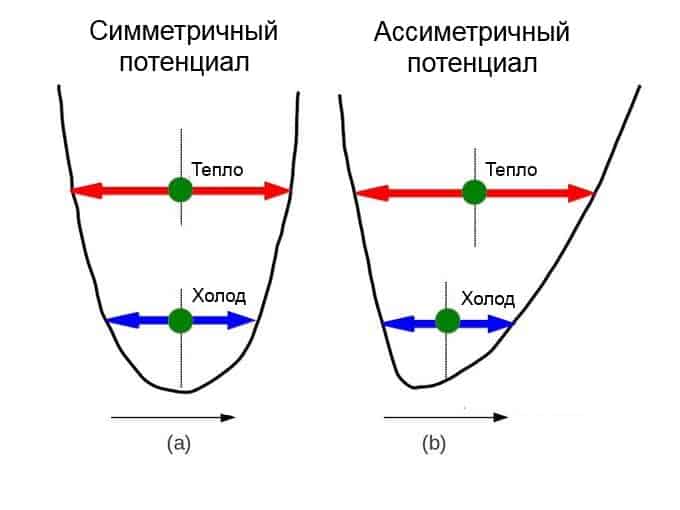
Типичный межчастичный потенциал в конденсированном веществе

Энергетическое обследование проектируемых режимов работы системы теплоснабжения

При проектировании система теплоснабжения ЗАО «Термотрон-завод» была рассчитана на максимальные нагрузки.

Система проектировалась на 28 потребителей тепла. Особенность системы теплоснабжения в том, что часть потребителей тепла от выхода котельной до главного корпуса завода. Далее потребитель тепла — главный корпус завода, и затем остальная часть потребителей располагается за главным корпусом завода. То есть главный корпус завода является внутренним теплопотребителем и транзитом подачи тепла для последней группы потребителей тепловой нагрузки.

Котельная проектировалась на паровые котлы ДКВР 20-13 в количестве 3 штук, работающие на природном газе, и водогрейные котлы ПТВМ-50 в количестве 2 штук.

Одним из важнейших этапов проектирования тепловых сетей являлось определение расчетных тепловых нагрузок.

Расчетный расход тепла на отопление каждого помещения можно определить двумя способами:

— из уравнения теплового баланса помещения;

— по удельной отопительной характеристике здания.

Проектные значения тепловых нагрузок производился по укрупненным показателям, исходя из объема зданий по фактуре .

Расчетный расход тепла на отопление i-го производственного помещения , кВт, определяется по формуле:

, (1)

где: — коэффициент учета района строительства предприятия:

(2)

где — удельная отопительная характеристика здания, Вт/(м3.К);

— объем здания, м3;

— расчетная температура воздуха в рабочей зоне, ;

— расчетная температура наружного воздуха для расчета отопительной нагрузки, для города Брянска составляет -24.

Определение расчетного расхода тепла на отопление для помещений предприятия производилось по удельной отопительной нагрузке (табл. 1).

Таблица 1Расходы тепла на отопление для всех помещений предприятия

№ п/п	Наименование объекта	Объем здания, V, м3	Удельная отопительная характеристика q_0,Вт/м3К	Коэффициент е	Расход тепла на отопление , кВт
1	Столовая	9894	0,33	1,07	146,58
2	Малярка НИИ	888	0,66	1,07	26,46
3	НИИ ТЭН	13608	0,33	1,07	201,81
4	Сборка эл. двигателей	7123	0,4	1,07	128,043
5	Модельный участок	105576	0,4	1,07	1897,8
6	Окрасочное отделение	15090	0,64	1,07	434,01
7	Гальванический отдел	21208	0,64	1,07	609,98
8	Заготовительный участок	28196	0,47	1,07	595,55
9	Термический участок	13075	0,47	1,07	276,17
10	Компрессорная	3861	0,50	1,07	86,76
11	Приточная вентиляция	60000	0,50	1,07	1348,2
12	Пристройка отдела кадров	100	0,43	1,07	1,93
13	Приточная вентиляция	240000	0,50	1,07	5392,8
14	Тарный цех	15552	0,50	1,07	349,45
15	Заводоуправление	3672	0,43	1,07	70,96
16	Учебный класс	180	0,43	1,07	3,48
17	Техотдел	200	0,43	1,07	3,86
18	Приточная вентиляция	30000	0,50	1,07	674,1
19	Заточный участок	2000	0,50	1,07	44,94
20	Гараж — Лада и ПЧ	1089	0,70	1,07	34,26
21	Литейка /Л.М.К./	90201	0,29	1,07	1175,55
22	Гараж НИИ	4608	0,65	1,07	134,60
23	Насосная	2625	0,50	1,07	58,98
24	НИИ	44380	0,35	1,07	698,053
25	Запад — Лада	360	0,60	1,07	9,707
26	ЧП «Кутепов»	538,5	0,69	1,07	16,69
27	Лесхозмаш	43154	0,34	1,07	659,37
28	АО К.П.Д. Строй	3700	0,47	1,07	78,15

ИТОГО ПО ЗАВОДУ:

Расчетный расход тепла на отопление ЗАО «Термотрон-завод» составляет:

Суммарные тепловыделения для всего предприятия составляют:

Расчетные теплопотери для завода определяются, как сумма расчетного расхода тепла на отопление всего предприятия и суммарных тепловыделений, и составляют:

Расчет годового расхода тепла на отопление

Так как предприятие ЗАО «Термотрон-завод» работало в 1 смену и с выходными днями, то годовой расход тепла на отопление определяется по формуле:

(3)

где: -средний расход тепла дежурного отопления за отопительный период, кВт (дежурное отопление обеспечивает температуру воздуха в помещении);

, — число рабочих и нерабочих часов за отопительный период соответственно. Число рабочих часов определяется перемножением продолжительности отопительного периода на коэффициент учета числа рабочих смен в сутках и числа рабочих дней в неделю.

Предприятие работает в одну смену с выходными.

(4)

Тогда

(5)

где: -средний расход тепла на отопление за отопительный период, определяемый по формуле:

. (6)

Вследствие не круглосуточной работы предприятия, рассчитывается нагрузка дежурного отопления для средней и расчетной температур наружного воздуха, по формуле:

; (7)

(8)

Тогда годовой расход тепла определяется:

График скорректированной отопительной нагрузки для средней и расчетной температур наружного воздуха:

; (9)

(10)

Определим температуру начала — конца отопительного периода

, (11)

Таким образом, принимаем температуру начала конца отопительного периода =8.

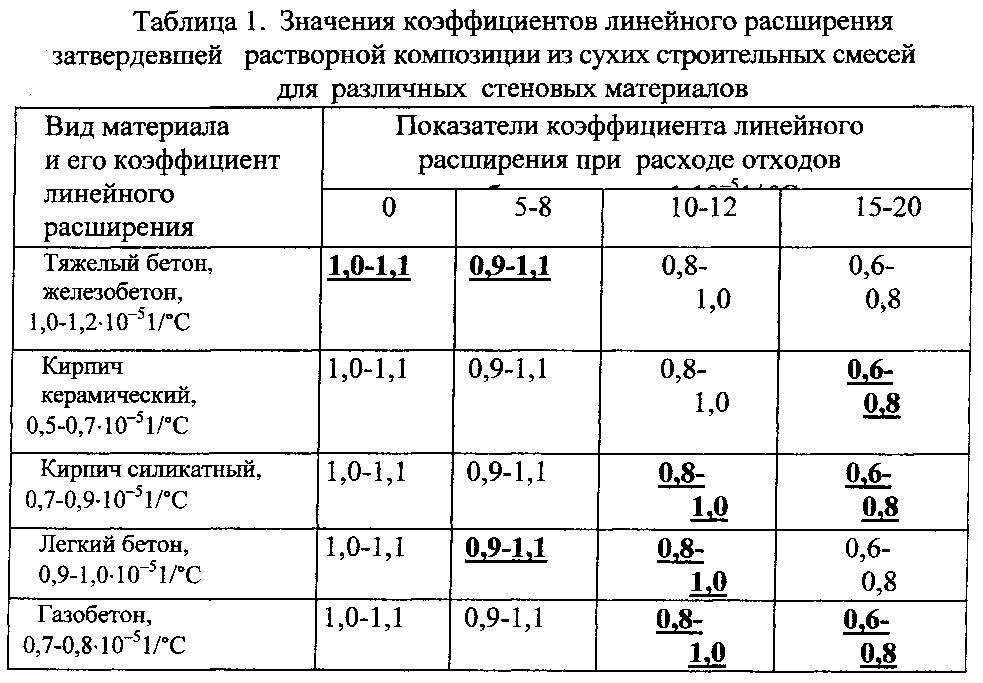
Теплофизические свойства бетонов

Образцы с разной теплофизикой Основные свойства бетона, связанные с воздействием на него тепловой энергии, это теплоемкость, теплопроводность и весьма важный в сфере строительства коэффициент линейного расширения. Без учета данных характеристик бетона невозможно добиться создания прочной конструкции здания, не склонной к разрушению под воздействием температурных колебаний.

Теплопроводность.

Теплопроводность бетона играет существенное значение при определении его строительно-физических качеств. Уровень теплопроводности зависит от структуры составляющих бетона и его строения в целом. Да значение данной характеристики оказывает влияние несколько факторов, среди которых наибольшее значение имеют влажность бетона и его температура. Чем большее количество влаги будет содержаться в бетоне и чем до большей температуры он будет нагрет, тем большей теплопроводностью он будет обладать

При проведении практических расчетов во внимание также принимается значение интегральной пористости. Смысл этого показателя состоит в определении объемного веса бетона при температуре +25С в высушенном до неизменяемого веса состоянии (рис

1).

Таблица теплопроводности

Кроме того, в строительной практике также может быть использована для расчета теплопроводности формула Б. Н. Кауфмана:

где под корнем стоит фиксированный коэффициент при указанных выше условиях: +25С и полная просушка. Измеряется это значение в ккал/м-ч-град, для высушенного бетона объемный вес выражается в т/м3.

Между тем, приведенная формула не может быть признана единственно верным способом расчета теплопроводности бетона, т.к. в ней не учитываются показатели пористости бетона, т.е. данные о распределении пор по типоразмеру, о степени сообщаемости или замкнутости. Поэтому с помощью данной формулы наиболее близкие к фактической действительности данные можно получить лишь в том случае, когда на стройке используются бетоны одинакового строения и созданные на заполнителях идентичного строения. Приводить здесь и использовать на практике универсальную и наиболее точную формулу для вычисления фактического уровня теплопроводности бетона не имеет смысла, поскольку она учитывает абсолютно все характеристики бетона. Получить подобные данные в условиях индивидуального жилищного строительства весьма проблематично, да и бессмысленно, т.к. при малых масштабах стройки и небольших конструкционных нагрузках небольшая ошибка в значении теплопроводности бетона особой роли не играет.

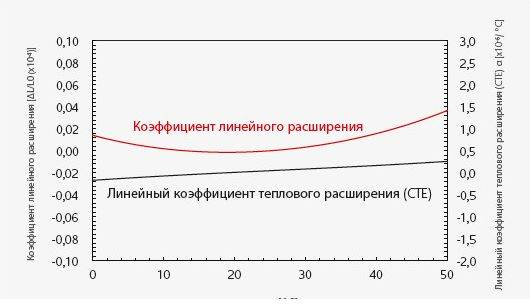
Коэффициент температурного расширения и теплоемкость бетона.

Под коэффициентом температурного расширения бетона в строительной практике принято понимать величину отклонения физических размеров бетона при изменении его температуры. Если упростить определение, то коэффициент расширения помогает определить, насколько увеличатся длина и ширина бетонного блока, если температура воздуха повысится на сколько-то градусов. Непринятие в расчет этого показателя моет привести к разрушениям возведенных из бетона конструкций при сезонных колебаниях температур.

Тепловое расширение способно привести к растрескиванию

Показатели коэффициентов температурного расширения бетона и стали приблизительно одинаковы, что широко используется при создании железобетонных конструкций высокой прочности.

От показателя теплоемкости бетона зависит скорость прогрева бетона до нужной температуры, а значит, и до нужных физических характеристик. Без учета теплоемкости зачастую попросту невозможно рассчитать время подачи жидкого бетона на объект строительства, особенно в холодное время года. Обычное значение этого показателя для большинства распространенных марок бетона колеблется в пределах от 0,28 до 0,33 ккал/кг .

Влияние теплового расширения на разные материалы

Хрупкие материалы

В приведенных выше примерах мы увидели, насколько важно оставлять пространство для расширения при работе с материалами с высоким коэффициентом теплового расширения. В некоторых случаях материалы бывают настолько хрупкими, что разрушаются при резком повышении температуры, даже если могут спокойно двигаться в окружающих их конструкциях

Обычно это происходит, если тело неравномерно нагревается или охлаждается. В этом случае объем также уменьшается или увеличивается неравномерно, и в результате вызванного этим напряжения тело растрескивается или разрушается. Так происходит, например, с изделиями из стекла и керамики.

Для предотвращения термического удара материалы иногда усиливают. При этом внутри них возникают напряжения, обратные деформирующей силе. В некоторых случаях помогают также постепенные нагрев или охлаждение — это позволяет хрупким материалам расширяться постепенно, с минимальным напряжением.

Крышка из закаленного стекла разбивается на мелкие осколки

Коэффициент теплового напряжения материала можно понизить методом комбинирования его с материалом с более низким коэффициентом. Кроме этого коэффициент можно изменить механически, в процессе производства — так делают при изготовлении закалённого стекла. Стекло нередко закаляют после того, как придали ему необходимую форму, иначе оно легко разрушается, если применить к нему силу, например при его резке. Это происходит вследствие возникновения распределенных механических напряжений по объему стеклянного предмета в процессе закалки стекла с помощью нагревания и охлаждения или во время химической обработки.

Для повышения безопасности задние и боковые стекла в автомобилях делают из закаленного стекла. Для еще большей безопасности лобовое стекло состоит из двух слоев закаленного стекла, приклеенных к пленке между ними. Если такое стекло разбить, то осколки остаются на пленке.

Примеры материалов, которые выдерживают высокие температуры и большие перепады температур — закаленные стекло и керамика. Чаще всего их обрабатывают так, чтобы взаимодействие сил по поверхности с силами внутри изделия ограничивало движение молекул с увеличением температуры, и тем самым предотвращало структурную нагрузку, которая обычно присутствует в необработанных стекле и керамике. Обработка бывает механической и химической. Закаленные стекло и керамика растрескиваются при температурах, намного выше температур для необработанных керамики и стекла. Закаленные материалы прочнее обычных, поэтому их нередко используют там, где материалы должны выдерживать большие нагрузки.

Если же закаленное стекло все-таки разбивается, то оно растрескивается на мелкие осколки, а не на большие, как бывает с обычным стеклом. Благодаря этому, закаленное стекло более безопасно и его используют там, где велика вероятность, что это стекло разобьется. Например, чтобы защитить водителя и пассажиров от травм большими осколками стекла в случае аварии, в автомобилях используют именно закаленное стекло.

У некоторых хрупких материалов очень интересные свойства. Хороший пример — изделие из стекла в форме капли, с длинным «хвостом», которое можно сделать, капнув расплавленное стекло в ведро холодной воды. Свойства такого стекла напоминают свойства закаленного стекла. Иногда стекло такой формы называют каплями Принца Руперта

. Во время охлаждения, наружный слой таких капель охлаждается намного быстрее, чем внутренняя часть, поэтому стекло сжато вовнутрь, то есть давление внутри намного больше, чем давление наружного слоя. В результате такая капля хранит большую потенциальную энергию. Благодаря такому распределению сил в капле, более широкая ее часть выдерживает большое напряжение, даже удар молотком. Хвост капли, наоборот, очень хрупок, и если его повредить, то вся капля разлетается на мелкие осколки. Это очень похоже на миниатюрный взрыв. Обычное закаленное стекло нельзя резать после обработки по аналогичным причинам. На сайте YouTube есть множество захватывающих видео взрыва капель Принца Руперта, записанных на высокой скорости 100 000 кадров в секунду и выше.

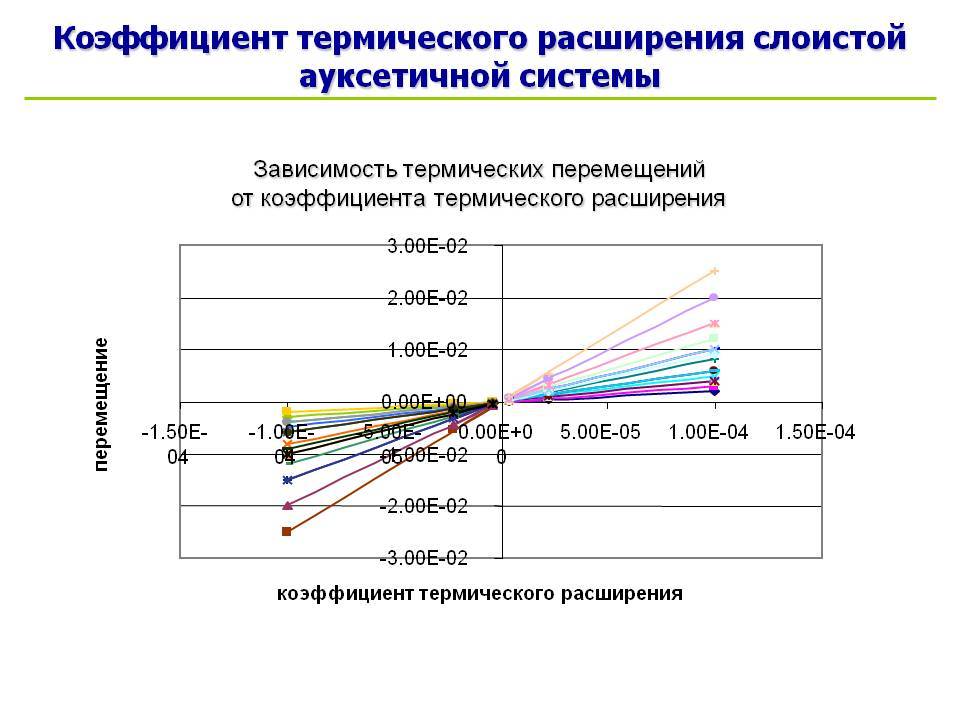
1.5. Температурные перемещения

Вернемся к бруску материала, показанного на рисунке 1 . Предполагаем, что материал бруска является гомогенным и изотропным, то есть механические свойства материала бруска являются одинаковыми во всем его объеме. Кроме того, предполагаем, что изменение температуры ΔT

является однородным, то есть одинаковым, по всему бруску. При таких условиях мы можем вычислить увеличение любого размера бруска путем умножения первоначального размера на температурную деформацию. Например, если один из размеров бруска составляет L, то этот размер увеличиться на величину

δТ = εT·L=α·ΔT·L (4) Уравнение (4) можно применять для вычисления изменений длин элементов конструкций после однородного нагрева, например, удлинение призматического стержня на рисунке 2.2. Поперечные размеры стержня также изменятся, но эти изменения не показаны на рисунке 2.2, так как обычно они не оказывают влияния на осевые силы, которые передаются этим стержнем.

Рисунок 2.2 – Увеличение длины призматического стрежня в результате однородного увеличения температуры (уравнение (4))

Пример.

Оценим удлинение незакрепленных алюминиевого и стального стержней длиной 3 м при увеличении их температуры на 50 ºС.

Для алюминиевого стержня:

δТ =α·ΔT·L = 23·10-6·50·3000 = 3,5 мм Для стержня из малоуглеродистой стали:

δТ =α·ΔT·L = 12·10-6·50·3000 = 1,8 мм При рассмотрении выше температурных деформаций предполагалось, что конструкция не имеет ограничений для своих перемещений, что позволяло ей расширяться или сокращаться совершенно свободно. Такие условия возникают, например, когда объект лежит на гладкой поверхности, на которой не возникает трения . В таких случаях при однородном нагреве всего объекта в целом не возникает напряжений, хотя неоднородные изменения температуры могут вызывать внутренние температурные напряжения. Однако многие конструкции имеют опоры, которые препятствуют свободному расширению и сокращению их размеров. Поэтому в них развиваются температурные напряжения даже, если изменение температуры является однородным по всей конструкции.